среда, 11 марта 2009 г.

Скользящая корреляция [090311_04]

В проведенном эксперименте исследовались изменения по корреляции в разных частях ряда. В предыдущих экспериментах (см. Корреляция по относительному изменению [090311_02] и Корреляция масштабированного относительного изменения [090311_03]) корреляция рассчитывалась за весь период тестирования (1000 последних дней), но не исследовалось как она меняется. В данном эксперименте смотрим на изменение зависимостей.

Здесь корреляция высчитывалась в каждом тестовом дне на основе данных предыдущих 20 дней. Всего тест проведен на 1000 последних дней. Зависимость показана только для Сбербанка.

Для сравнения на графики наложена линия (красным пунктиром) соответствующая уровню корреляции для всего тестового диапазона.

Общий вывод по эксперименту - зависимости постоянно меняются. Искать какую-либо закономерность на длительном диапазоне не получится. Придется оперировать короткими выборками.

См.: Относительное изменение, Корреляция
на 16:12 0 коммент.

Корреляция масштабированного относительного изменения [090311_03]

В предыдущем эксперименте (см. Корреляция по относительному изменению [090311_02]) относительные изменения брались без масштабирования. На рисунке ниже повторяем его результаты.


В данном эксперименте произведем масштабирование данных. Только сделаем это без применения сигмоидного преобразования. Будем только делить на стандартное отклонение рассчитываемое с лагом в 10 дней. Результаты на рисунке ниже.


Отличия хотя и слабые, но заметно снижение зависимости.

См.: Относительное изменение, Корреляция, Масштабирование
на 15:03 0 коммент.

Корреляция по относительному изменению котировок ММВБ [090311_02]

В данном эксперименте смотрим на связанность относительных изменений различных котировок закрытия ММВБ и некоторых мировых индексов. Оценку производим по корреляции. Ниже в таблице приведены данные для диапазона в 1000 последних дней.


 sber sberp sngs rtkm gmkn msng sibn lkoh
sber 1,00 0,88 0,67 0,43 0,65 0,49 0,63 0,74
sberp 0,88 1,00 0,67 0,36 0,61 0,50 0,62 0,71
sngs 0,68 0,68 1,00 0,40 0,63 0,48 0,62 0,78
rtkm 0,39 0,37 0,39 1,00 0,42 0,32 0,39 0,43
gmkn 0,65 0,61 0,63 0,42 1,00 0,42 0,63 0,69
msng 0,48 0,49 0,48 0,34 0,42 1,00 0,47 0,49
sibn 0,62 0,62 0,62 0,40 0,63 0,48 1,00 0,75
eurusd 0,18 0,19 0,19 0,07 0,18 0,12 0,21 0,18
gbpusd 0,19 0,18 0,19 0,09 0,14 0,10 0,20 0,19
usdjpy 0,19 0,19 0,20 0,07 0,15 0,17 0,14 0,17
cac40 0,56 0,53 0,52 0,34 0,45 0,39 0,49 0,54
dax 0,51 0,49 0,50 0,35 0,44 0,38 0,45 0,49
micex 0,87 0,84 0,84 0,52 0,79 0,58 0,78 0,92
micex10index 0,86 0,85 0,87 0,52 0,77 0,58 0,75 0,88
nasdaq 0,28 0,28 0,34 0,16 0,23 0,20 0,22 0,22
sp500 0,29 0,29 0,34 0,16 0,25 0,22 0,25 0,24
djia 0,27 0,27 0,33 0,15 0,24 0,20 0,24 0,21
rtsi 0,80 0,77 0,76 0,49 0,73 0,52 0,74 0,84
gold 0,07 0,12 0,10 0,04 0,11 0,08 0,17 0,17
lkoh 0,75 0,71 0,78 0,42 0,69 0,49 0,75 1,00

Ниже на графиках даны срезы по таблице для каждой из исследуемых бумаг.








Практически все исследуемые бумаги имеют выраженную связанность (больше 0,5) с индексами ММВБ.

Все зависимости получились положительными. что свидетельствует об однонаправленном изменении.

Все бумаги имеют слабую связанность с валютами, золотом и американскими индексами.

Выбранный метод оценки имеет несколько недостатков. Среди них можно отметить - большой диапазон оценки (1000 дней) (за этот период наверняка зависимости менялись), не было применено масштабирование (на разных участках наверняка были разные амплитуды колебаний), ряды сравнивались без задержки во времени (по таким данным прогнозную модель не построить), оценка осуществлялась по корреляции (нельзя выявить криволинейные зависимости как в методе box-counting).

В дальнейших экспериментах можно будет исправить эти недостатки.

См.: Относительное изменение, Корреляция
на 13:07 0 коммент.

Корреляция

Коэффициент корреляции Пирсона. Существует несколько различных коэффициентов корреляции. Наиболее широко известен коэффициент корреляции Пирсона, характеризующий степень линейной зависимости между переменными. Он определяется, как:


Эксперименты:

Корреляция по относительному изменению [090311_02]
Корреляция масштабированного относительного изменения [090311_03]
Скользящая корреляция [090311_04]

Ссылки:

http://alglib.sources.ru/statistics/correlation.php

на 12:09 0 коммент.

Масштабирование относительного изменения [090311_01]

В данном эксперименте берем исходный ряд котировки закрытия Лукойла за последние 1000 дней (левый верхний график). Вычисляем относительное изменение (средний верхний график). Вычисляем для него стандартное отклонение, делим на него и берем сигмоид. Получаем масштабированный ряд (правый верхний график). В связи с тем, что амплитуда колебаний ряда различна на разных участках получаем такое неравномерное заполнение. Для дальнейшего использования в прогнозном элементе такой ряд несет мало информации. Необходимо подавать ряды которые максимально равномерны и заполняют весь диапазон от 0 до 1.

Для устранения этого дефекта будем на каждом участке ряда вычислять амплитуду колебаний. В качестве амплитуды возьмем стандартное отклонение с некоторым лагом (левый нижний график). Здесь лаг взят равным 10 дням. Далее делим относительное изменение на амплитуду и получаем новый график для относительного изменения (центральный нижний график). Не трудно заметить, что здесь амплитуда сигнала приблизительно одинакова на всем протяжении ряда. Далее пропускаем через сигмоид и получаем масштабированный ряд (правый нижний график).

Полученый ряд значительно выигрывает по отношению к предыдущему. Он более равномерен и заполняет почти весь диапазон от 0 до 1.
На данном рисунке представлена схема процесса по масштабированию относительного изменения от сигнала. На входе имеем сигнал. На выходе имеем амплитуду и масштабированный сигнал пригодный для дальнейшей обработки.

См.: Стандартное отклонение, Сигмоид, Относительное изменение, Масштабирование

на 10:44 0 коммент.

Масштабирование

Для обработки данных в единой модели необходимо приводить их к одному масштабу измерений.

Обычно данные приводят к диапазону от 0 до 1.

Эксперименты:
Масштабирование относительного изменения [090311_01]

на 10:00 0 коммент.

вторник, 10 марта 2009 г.

Стандартное отклонение

Стандартное отклонение (иногда среднеквадратичное отклонение) — в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах измерения самой случайной величины. Равна корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

s=\sqrt{\frac{n}{n-1}\sigma^2}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \quad \sigma=\sqrt{\frac{1}{n}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}

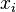где s\,\! — стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклонения случайной величины X относительно её математического ожидания; \sigma^2\,\! — дисперсия; x_i\,\! — i-й элемент выборки; \bar{x}\,\! — среднее арифметическое выборки; n\,\! — объём выборки.


Ссылки:

http://ru.wikipedia.org/wiki/Выборочное стандартное отклонение

Эксперименты:


на 17:37 0 коммент.

Применение сигмоида к нормальному распределению [090310_04]


Взят случайный сигнал с нормальным распределением (левый верхний график). Распределение для него показано рядом (правый верхний график). К сигналу применено сигмоидное преобразование (левый нижний график). В результате имеем более красивое распределение близкое к равномерному (правый нижний график).

См.: Сигмоид, Относительное изменение
на 15:51 0 коммент.

Применение сигмоидного преобразования к относительному изменению [090310_03]


В данном эксперименте к относительному изменению курса закрытия (левый верхний график) применено сигмоидное преобразование (левый нижний график). Для обоих рядов показана гистограмма распределений.
Для исходного ряда показано стандартное отклонение. Вычисления производились для курса закрытия Лукойл за последние 1000 дней.
Из распределений видно, что после преобразования данные имеют вид более похожий на равномерный.

См.: Сигмоид, Относительное изменение
на 15:19 0 коммент.

Сигмоид

Сигмоид - математическое преобразование приводящее нормально распределенные данные к равномерному виду.

Приведение к равномерному распределению используется в предобработке данных перед подачей сигнала на нейронные сети.

Теория:
http://www.intuit.ru/department/expert/neurocomputing/7/3.html

Эксперименты:
Применение сигмоида к нормальному распределению [090310_04]
Применение сигмоидного преобразования к относительному изменению [090310_03]

на 15:12 0 коммент.

Применение относительного изменения к котировкам ММВБ [090310_02]


В данном эксперименте берем 1000 последних дней закрытия курса Лукойл. На верхнем левом рисунке представлен его график. Справа сверху представлена гистограмма распределения этого курса.
Ниже представлен график относительного изменения курса и его гистограмма. Как видно из результатов, гистограмма относительного изменения близка к нормальному виду.

См. Относительное изменение

на 14:34 0 коммент.

Относительное изменение

Относительное изменение — метод математического преобразования абсолютных значений временного ряда. Используется при прогнозировании временных рядов.

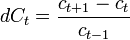
{dC_{t}} = {\frac {c_{t+1}-c_t} {c_{t-1}}}

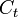где: ~C_t - абсолютное значение ряда в точке 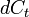~t, ~{dC_{t}} - относительное изменение в точке ~{t}.

Эксперименты:
Применение относительного изменения к котировкам ММВБ [090310_02]

Ссылки:
http://ru.wikipedia.org/wiki/Относительное_изменение

на 13:44 0 коммент.

Влияние на норму box-counting кол-ва тестов и разбиений [090310_01]


В данном эксперименте исследуем зависимость нормы box-counting от количества разбиений и количества тестовых примеров.
Не трудно заметить, что имеем растущую зависимость от обоих параметров.
Для разных функционалов зависимость находится на разных уровнях.
Чем сильнее зависимость, тем выше находится поверхность.
Ни каких экстремумов не наблюдается. Так что для простоты вычислений для выбранных функционалов разбиения и кол-во примеров можно большие не выбирать.
В данном эксперименте разбиения брались до 200, а количество примеров до 1000.

Дополнительно были расширены диапазоны разбиений и кол-ва тестов до 2000. Было замечено неограниченное возрастание нормы box-counting при возрастании кол-ва примеров и ограниченное возрастание при росте кол-ва разбиений. Это можно видеть на растущих линиях вдоль оси test_cnt (количество примеров) и почти горизонтальных линиях вдоль оси N (кол-во разбиений).
Значит предел нормы определяется количеством примеров.

См. Метод box-counting
на 11:55 0 коммент.

Влияние кол-ва разбиений на норму box-counting [090304_02]


В данном эксперименте исследуем норму box-counting в зависимости от количества разбиений для различных функционалов.
В пределе (стремлении кол-ва разбиений к бесконечности) нормы водят к одинаковому значению. Но там где зависимости слабее графики проходят ниже.
Чем меньше разбиений тем ниже значение нормы. Напрашивается вывод о несущественности кол-ва разбиений. Для выбранных функционалов лучший можно выбирать при любом значении разбиений. Для простоты расчетов кол-во разбиений лучше брать малым.

См. Метод box-counting
на 11:02 0 коммент.
Подписаться на: Сообщения (Atom)