В данном эксперименте исследуем зависимость нормы box-counting от количества разбиений и количества тестовых примеров.
Не трудно заметить, что имеем растущую зависимость от обоих параметров.
Для разных функционалов зависимость находится на разных уровнях.
Чем сильнее зависимость, тем выше находится поверхность.
Ни каких экстремумов не наблюдается. Так что для простоты вычислений для выбранных функционалов разбиения и кол-во примеров можно большие не выбирать.
В данном эксперименте разбиения брались до 200, а количество примеров до 1000.
Дополнительно были расширены диапазоны разбиений и кол-ва тестов до 2000. Было замечено неограниченное возрастание нормы box-counting при возрастании кол-ва примеров и ограниченное возрастание при росте кол-ва разбиений. Это можно видеть на растущих линиях вдоль оси test_cnt (количество примеров) и почти горизонтальных линиях вдоль оси N (кол-во разбиений).
Значит предел нормы определяется количеством примеров.
См.
Метод box-counting
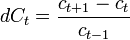
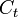- абсолютное значение ряда в точке 
, 
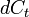- относительное изменение в точке 
.
